蒙特卡罗、动力学蒙特卡罗、分子动力学三者的异同解析

说得更直白一点，传统的MD和MC基本上是在干同一件事：算积分。只不过最早的MD是在微正则系综（NVE系综）里算积分，而最早的MC是在正则系综（NVT系综）里算积分。

先说MC

众所周知，正则系综里相空间的概率分布就是玻尔兹曼分布

其中H是体系的哈密顿量， 是配分函数， . 以一维线性谐振子为例 ，这个相空间概率分布就是下图所示，其实就是个高斯分布。

知道了概率分布，那么正则系综中任意平衡态热力学量M的系综平均 就是下面这个积分

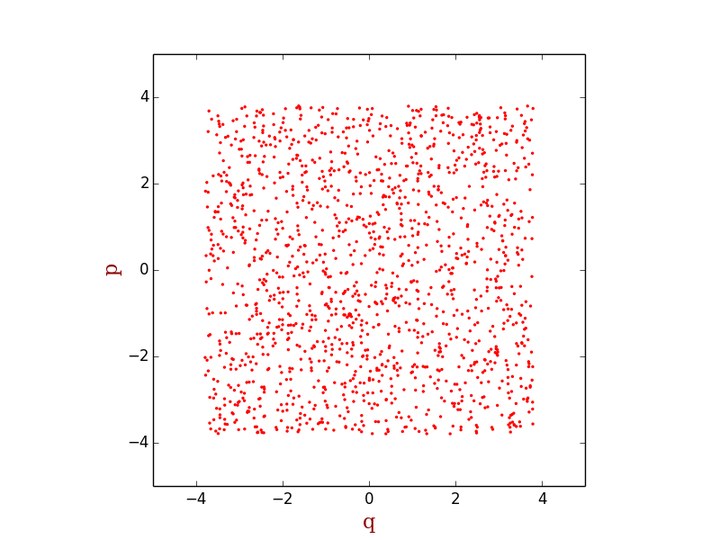
对于上式中的积分，绝大多数情况下是没有解析解的，因此只能通过数值求解。最简单粗暴的用蒙特卡洛方法求解上式积分的方法就是在整个积分区域上均匀地随机打点，求得每一点处的M(p,q)e^-ßH(p,q)值，然后对所有点求和再除以配分函数即可。例如对于一维线性谐振子，我们可以如下在相空间上均匀地打点

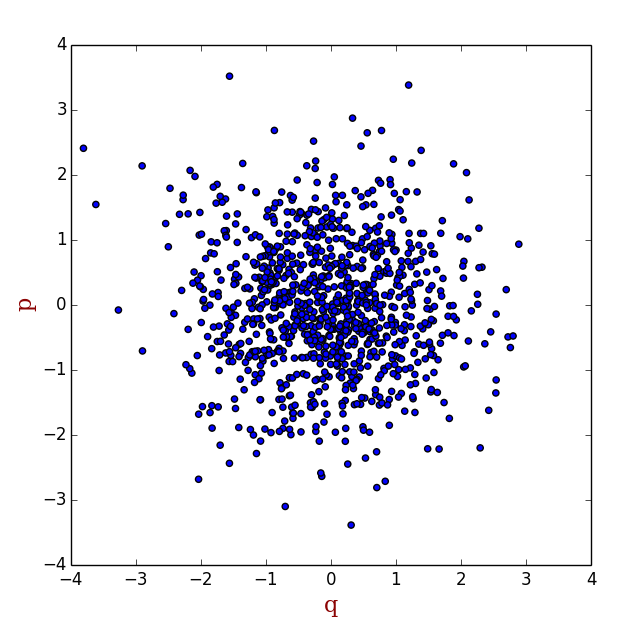
这种算法，的确非常简单，但效率很低。因为位于相空间中e^-ßΗ的值非常小的区域，系统处于这个区域的概率非常低，也就是说这些区域大体上来说对系综平均 的贡献是非常小的，然而在采样过程中，由于我们是随机均匀打点，这样e^-ßΗ的值非常小的点和e^-ßΗ的值非常大的点的权重是一样的。换句话说，我们浪费了不少时间在那些权重很小的点上。那么是否有这样算法，能够使产生的点的分布符合玻尔兹曼分布，也就是说，在e^-ßΗ的值非常小的区域少打点，在e^-ßΗ的值非常大的区域多打点（如下图所示），然后把每一点处的M值相加，就能得到我们需要的系综平均呢？Metropolis算法就是为了实现这样的目标产生的。关于Metropolis算法的细节，我不在这里展开，很多书籍里都有描述。

再说MD

MD是基于牛顿方程的，而从牛顿方程是可以很自然导出孤立体系在保守力作用下是能量守恒的，因此最初的MD是在微正则系综(NVE)里计算系综平均。根据统计力学的等概率假设，对于总能量为E的微正则系综，其相空间概率密度分布为P(p,q)=1/Ω(E)，其中Ω(E)是体系处于能量为E时的态密度(density of state)
那么热力学量M在微正则系综里的系综平均 就是
其中V是积分的区域，也就是当能量为E时系统所占据的相空间。拿一维线性谐振子作为例子，当能量为E时其在相空间中区域对应于下图中的圆环，那么这个系综平均就是根据上式在对应于能量为E的圆环区域上进行积分。MD所做的，就是让粒子跑遍这个圆环上的每一个点（历经各态，ergodicity)，把每一点上M的值加起来求平均，得到的就是系综平均(time average equals ensemble average, this is what we call ergodicity)。

综上，MD和MC都可看作是为计算系综平均的采样方法。采用Metropolis算法的MC不局限于在正则系综里的采样，可以应用于其他系综，比如NPT和巨正则系综。至于微正则系综，理论上也可以使用Metropolis算法，只是由于各个态之间能量相等，概率也相等，这时使用Metropolis算法不能起到加速采样的作用，等于白用。同样地，MD的采样也不局限于微正则系综，当把一个孤立体系和一个恒温器(thermostat)或者恒压器(barostat)耦合起来，就可以进行正则系综或者NPT系综里的模拟。当然，如果耦合的恒温器或者恒压器是以extended Lagrangian形式实现的话（比如Nose-Hoover Thermostat)，广义上来讲MD模拟还是可看作在一个大的微正则系综中进行。

MD和MC的比较

1、算法的难易程度。一般说来，MD的算法比MC要复杂一些。这是因为，对于MC而言，每产生一帧新的构型只要计算能量然后根据acceptance ratio移动粒子就足够了。但对于MD，每产生一帧新的构型所需要的不只是能量，还需要每个粒子的速度和受力来对牛顿运动方程进行数值积分，这就加大了计算量。如果还要考虑为了提高计算效率的Verlet neighbor list等设置，MD的算法会更复杂一些。

2、所能计算性质的多少。很明显，MD能比MC计算更多的性质，MC只能计算一些与动力学无关的平衡态性质，比如能量、比热容等等，MD既可以计算与动力学无关的性质，也可以计算与动力学相关的性质，比如扩散系数、热导率、黏度、态与态之间的跃迁速率，光谱等等。这是因为，使用Metropolis算法的MC，为了快速得到平衡态的分布，把整个系统简化为一条马尔可夫链，第N个构型只和第N－1个构型有关联，与第N－2或者更早的构型没有什么关联。在实际情况中不是这样的，系统是有记忆的，在t ₀时刻处于相空间中(p ₀,q ₀)点的系统与在t ₁时刻处于(p ₁,q ₁)的系统是有关联的，它们之间的关联可以用条件概率P(p ₁,q ₁;t ₁|p ₀,q ₀;t ₀) 来描述。很多动力学性质都和这样的条件概率有关系，而MD产生的数据是可以计算这些概率分布的。所以世界上没有免费的午餐，MC虽然算法简单，但大体上只能计算静态性质，如果要计算动力学性质还是要上MD。

3、可使用的软件。可使用的MD的软件远多于MC的软件。我个人觉得很大程度上是由于MD能够计算的性质远比MC多，并且数据可视化后给人更多直观的感受。比如说，你可以把MD模拟蛋白质折叠的轨迹文件用软件可视化之后做成动画，动画就比较直观地演示了蛋白质结构随时间的变化。可是如果你用MC做同样一个体系的模拟，你把轨迹可视化之后看到的可能就是一堆原子像无头苍蝇一样乱动，最后稳定在某个构型附近。一般来讲，MD软件的开发也不难，一旦把积分牛顿方程的engine写好，往里面添加新的相互作用势并不难，这样每添加一点新的功能，MD软件就可以适用于更多的体系。相比起MD软件的百花齐放，分子模拟中学术界通用的MC软件并不多，很多课题组都是自己写MC代码，但适用范围仅限于自己研究的体系。

4、增强抽样(enhanced sampling)。这是分子模拟中的一个大坑，不管MD还是MC都会面临在系综中采样不足的问题。

KMC

Kinetic Monte Carlo(KMC)和主要模拟平衡态性质的MD和Metropolis MC相差就比较远了，它主要模拟系统随时间的演化而非平衡态性质。KMC的基本思想是把整个系统划分成若干个态(state)，并获得态与态之间单位时间的跃迁几率（这个可以通过分子模拟或者过渡态理论来计算），然后通过具体的算法决定每一步往哪一个态跃迁，就可以模拟系统在各个态之间随时间演化。我没有做过KMC的研究，并不太了解KMC的算法，仅仅粗略看过一两篇用KMC模拟扩散的文章。以下的例子是我粗浅的理解，可能不太准确。

我们想用KMC模拟粒子在二维晶格上的扩散，并求出扩散系数。假定在单位时间步长内，粒子只能跳到它最相邻的格点。如图所示，粒子某时刻处于A格点，那么粒子下一时刻只有可能跳到B,C,D,E格点，单位时间内粒子从A跳到这些格点的跃迁几率分别为rAB,rAC,rAD,rAE。结合这些跃迁几率，KMC的算法就可以通过生成随机数来决定粒子下一步所在的格点。在模拟足够长时间后我们可以算出粒子的均方位移(mean square displacement, MSD)， 均方位移和扩散系数成正比关系，因而可以求出扩散系数。

当粒子只能在一维情况下运动（即只能从A到B或者从A到D)，并且rAB=rAD， 这种情况下KMC其实就是在模拟一维随机游走(random walk)。

本文经授权转载自知乎刘书乐老师的回答：Metropolis蒙特卡罗方法、动力学蒙特卡罗方法、分子动力学方法这三种模拟方法有何特点与差异？

欧洲足球赛事 编辑整理。

材料人重磅推出材料计算解决方案，可提供包括第一性原理、分子动力学、流体力学等方面的计算模拟外围是什么意思 。如有需求，欢迎联系微信号：iceshigu，或点击链接提交需求，微信端可扫以下二维码提交。